
 |
Intrinsic Dynamics Domains (IDDs) |
What are Intrinsic Dynamics Domains (IDDs)?
Intrinsic Dynamics Domain (IDD) is a new method taking advantage of robust dynamics in a reduced dimension (from 3N- to N-dimensional; N is the number of residues) and identifying clusters of residues bearing high similarity of such robust dynamics. The dynamics here can be purely rigid-body motions (PC1), purely vibrational motions (by ANM (Atilgan, et al., 2001) and PCA_NEST (Yang, et al., 2009)) or a mixed vibrational and rotational motions (GNM (Bahar, et al., 1997)).
IDDs, the interfaces between IDDs (referred to ‘D-planes’) and the axes penetrating through the interface of IDDs (referred to ‘D-axes’) are determined in order as follows.
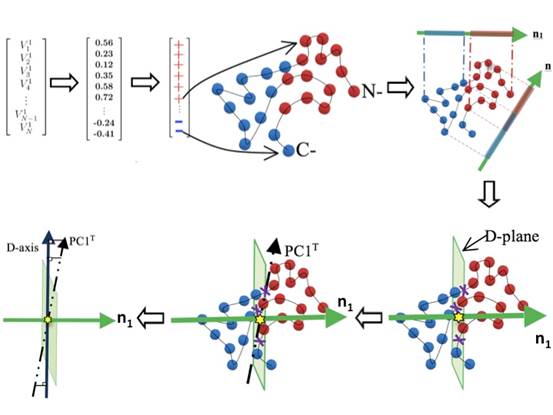
IDDs] The slowest normal mode V1 (either from GNM, or ANM/PCA in reduced dimension) is first obtained. Only the signs (+/-) of the numbers are kept and used to assign the dynamics properties of the protein residues. Nodes are in either red (‘+’ values in V1) or blue (‘-’ values in V1). According to their spatial distributions, spatially close residues with the same signs can be clustered into IDD. Only two largest clusters (IDDs) with opposite signs will be kept for the following analyses.
D-planes] To define a plane that best separates the two clusters, Linear Discriminant Analysis (LDA) is used. The method finds an axis (shown as n1) on which the projections of Res+ (in red) and Res- (in blue) can be best separated as compared to any other possible axis (e.g. nr on which the projections could overlap). The axis n1 found herein is called domain (D)-plane normal to define the D-plane (in light green) that goes through the geometric center of transition points, shown as the yellow star, which is usually close to the mass center. The transition points (in purple ‘x’ sign) are the centers of any two consecutive residues that have different dynamics properties in the primary sequence.
D-axes] We perform the Principal Component Analysis (PCA) on the transition points to find the largest principal component PC1T (shown as the broken line), onto which projections of transition points have the widest spread (see also Yang et al, 2009). The PC1T is then projected to the D-plane to obtain the D-axis (shown as the navy blue line). In our analyses, there is always one D-plane and one D-axis for every protein.
IDDs defined based on protein shape
IDDs can be defined based on geometry such that the interface (S-plane) separates the protein into two domains with the S-axis penetrating through the interface. The S-plane passes through the center of mass of protein thereby dividing the protein cross-wise into two domains. The first principal component of the distribution of Cα atoms in space forms S-plane normal. This S-axis is defined similar to the way in which D-axis is defined. As a figure skater rotates with her arms outstretched, her hands rotate in opposite directions. Similarly, if the protein rotates about any axis lying on the S-plane, residues rotating in opposite directions belong to two different domains defined by the protein shape.
What can IDDs do?
IDD reports groups of residues moving toward the same or opposite directions. The domains are formed differently in accord with the types of concerned dynamics.
So far, we found the protein-protein docking (PPD) orientation and enzyme catalytic sites are functions of IDDs.
PPD study -
Two proteins docking partners in an experimentally determined complex, are found to locate near the interface of the IDDs, and the axes threading through dynamics-transiting points of two proteins upon binding make an angle larger than 65 degree. The findings are used as screening criteria (D-planes cutting through binding partners and angles of D-axes > 40o) to cull dynamics-wise promising PPD decoys. Within the remained decoys that do fulfill our criteria, the chance to find near-native poses (hits) is >2.5 fold higher than a search without using such criteria.
Enzyme active-site study -
With similar criteria applied to find catalytic residues in enzymes, we found that the selected 50% of the residues, closest to the IDD interfaces, in an enzyme, can contain 90% of the total catalytic residues. This finding is different from previous studies suggesting a spherical search near the mass center of proteins can locate the binding sites. Our results show a more effective search would be directional (anisotropic; perpendicular to IDD interfaces) rather than spherical (isotropic). Proper comparisons of our results with those derived from random axes, planes as well as careful statistical assessments are carried out to address the significance of our data.
How does the IDD server work?
Please see the Help page for operational details. Basically, the IDD server takes a PDB file where atom coordinates in a protein structure are noted. IDD server first performs dynamics calculations using the physics models per users’ request. The server then clusters residues in similar dynamics into IDDs and then reports the locations and directions of D-planes and D-axes. The ‘similar’ dynamics are defined in one of the six slowest normal modes, per users’ request. The IDDs info can further be used to select promising PPD decoys against ZDOCK results. IDD server also reports the top 50% residues that are closest to the D-plane, which would contain ~90% of the catalytic residues in the uploaded enzyme structure. See Help page for more details.
Reference
The IDD work is done by Hongchun Li, Shun Sakuraba, Aravind Chandrasekaran and Lee-Wei Yang*. (2014) Molecular binding sites are located near the interface of intrinsic dynamics domains (IDDs).